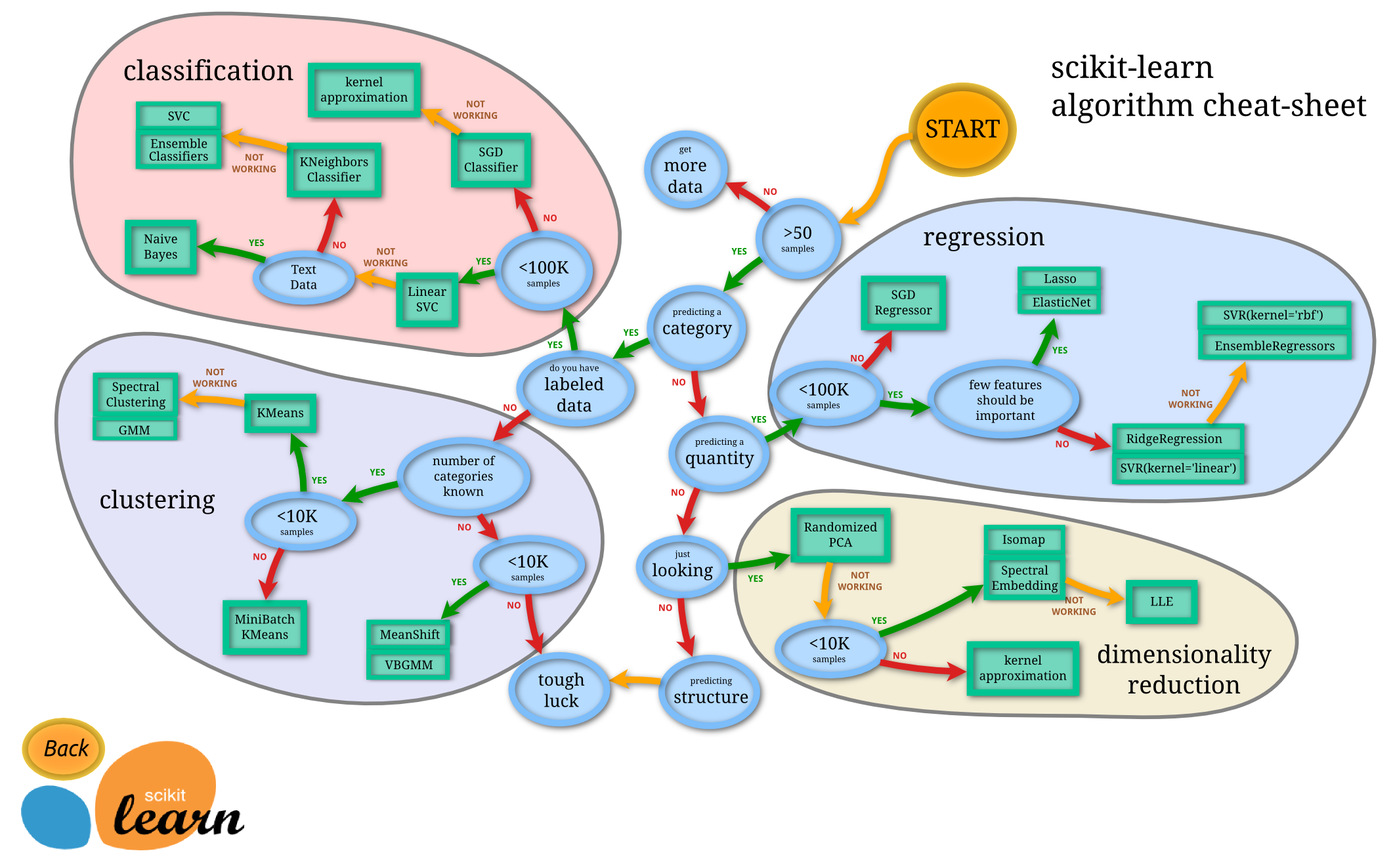
・regression 回帰モデル

線形回帰モデル 非線形回帰モデル ロジスティック回帰モデル

・dimensionality rduction 次元削減

主成分分析

・clustering クラスター分析

アルゴリズム (k近傍法,k-means法)

・classification 分類

サポートベクターマシーン

1.線形回帰モデル

教師あり学習 回帰問題の手法の中で最も基本的なモデル

線形→比例

パラメータの更新は最小二乗法で推定

目的変数Y と説明変数Xi, i = 1, ..., p および擾乱項ε の関係を以下のようにモデル化したものである。

$Y=β0+β1X1+β2X2+⋯+βpXp+ε  {\displaystyle Y=\beta _{0}+\beta _{1}X_{1}+\beta _{2}X_{2}+\cdots +\beta _{p}X_{p}+\varepsilon \ }$

特徴

・曲線的な相関は表現できないので不向き

・外れ値の影響を受けやすい

→Huber損失、Tukey損失を使うと外れ値の影響を受けにくくなる

・説明変数同士に相関があるといけない、推定値を歪ませてしまう

→多重共線性

・説明変数が多いと、上記の多重共線性が起きやすくなる。

　また過学習にもなりやすい

ハンズオン

線形回帰モデル-Boston Hausing Data-

2.非線形回帰モデル

線形回帰と違って、比例ではない

例えば

指数関数、対数関数、三角関数、冪関数、ガウス関数、ローレンツ曲線などがある。

●基底展開法 回帰関数として、基底関数と呼ばれる既知の非線形関数とパラメータベクトルの線型結合を使用 未知パラメータは線形回帰モデルと同様に最小2乗法や最尤法により推定

よく使われる基底関数 多項式関数,ガウス型基底関数,スプライン関数,Bスプライン関数

未学習と過学習

学習データに対して十分小さな誤差が得られないモデル　→　未学習 (対策) モデルの表現力が低いため、表現力の高いモデルを利用する。

小さな誤差は得られたけど、テスト集合誤差との差が大きいモデル　→　過学習(過剰適合) (対策１) 学習データの数を増やす。 (対策２) 不要な規定関数(変数）を削除して表現を抑止 (対策３) 正則化法を利用して表現力を抑止

ハンズオン

3.ロジスティック回帰モデル

ベルヌーイ分布に従う変数の統計的回帰モデルの一種

教師あり学習のひとつで分類問題(クラス分類）を扱うときに使用する

回帰とあるが分類なので注意

出力（目的変数）は1か0になる

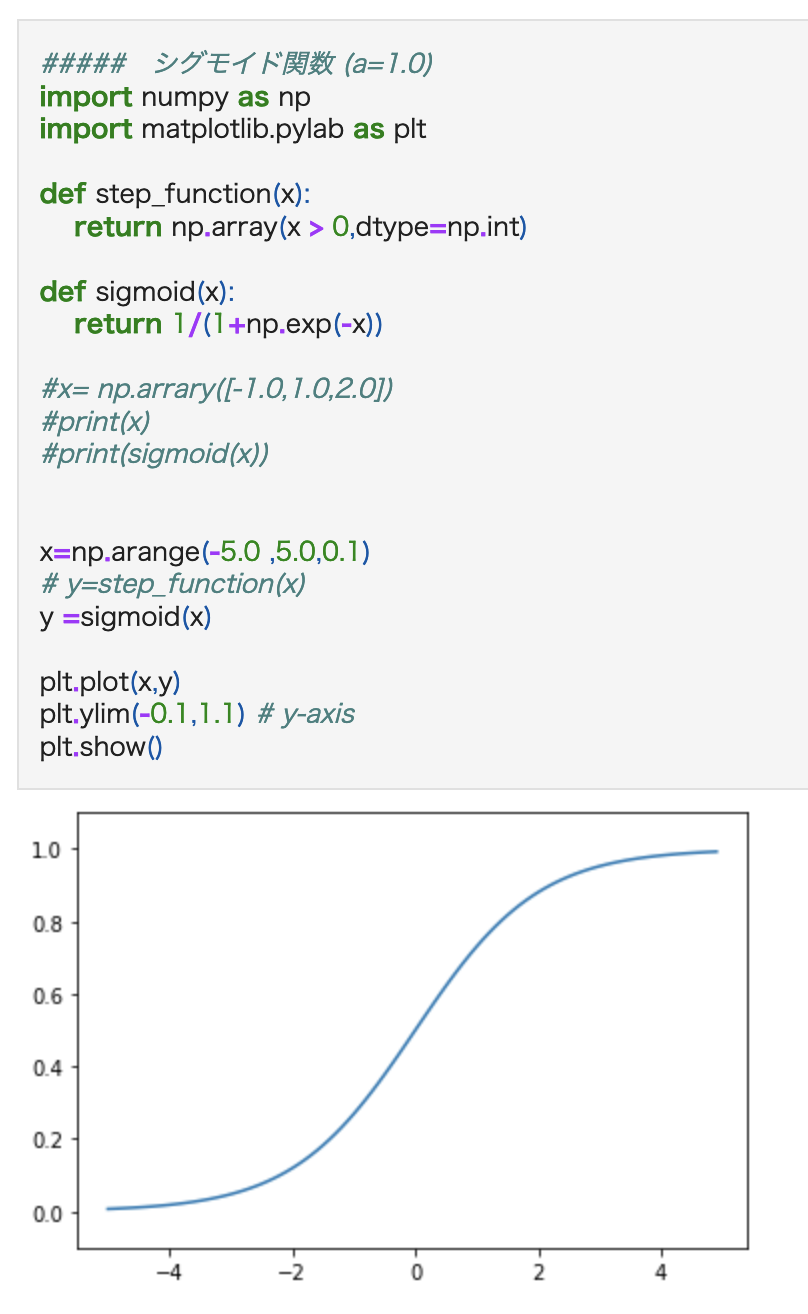
シグモイド関数

シグモイド関数の微分は、シグモイド関数自身で表現することが可能

下記の図のようになる

最尤推定

確率分布 (正規分布、t分布、ガンマ分布、一様分布、ディリクレ分布) ロジスティック回帰モデルではベルヌーイ分布を利用

確率的勾配降下法(SGD)

連続最適化問題に対する勾配法の乱択アルゴリズム。 目的関数が微分可能な和の形であることが必要。バッチ学習である最急降下法をオンライン学習に改良したもの。

評価方法(混同行列)

TP: 真陽性(True Positive) 　正しくpositiveと判別した個数 FP :偽陰性(False Positive) 　間違えてpositiveと判別した個数 TN :真陰性(True Negative) 　正しくNegativeと判別した個数 FN : 偽陽性(False Negative) 間違えてNegativeと判別した個数

・正解率：正解した数/ 予測対象となった全データ数

$\frac {TP+TN}{TP+FN+FP+TN}$

・再現率(Recall)：「本当にPositiveなもの」の中からPositiveと予測できる割合 $\frac {TP}{TP+FN}$ →　失敗が許されない現場で使用

・適合率(Precision)：　モデルが「Positiveと予測」したものの中で本当にPositiveである割合

$\frac {TP}{TP+FP}$

・Ｆ値(F value)　：適合率と再現率の中庸を取る

$\frac {2}{(\frac{1}{Precision} + \frac{1}{Recall}) }$

ハンズオン

タイタニック　生存予測

4.主成分分析

相関のある多数の変数から相関のない少数で全体のばらつきを最もよく表す主成分と呼ばれる変数を合成する多変量解析の一手法。データの次元を削減するために用いられる。

→

説明変数が多いと過学習してしまう可能性が高まってしまうので、目的変数への影響の高い説明変数以外は削減してしまう

分散が最大になるように圧縮する

ラグランジュ関数を微分して最適解を求める

$Var ( \bar {X} ) a_j = \lambda a_j$

主成分変換は行列の特異値分解とも結び付けられる。

ハンズオン

乳がん検査データ

5.アルゴリズム (k近傍法,k-means法)

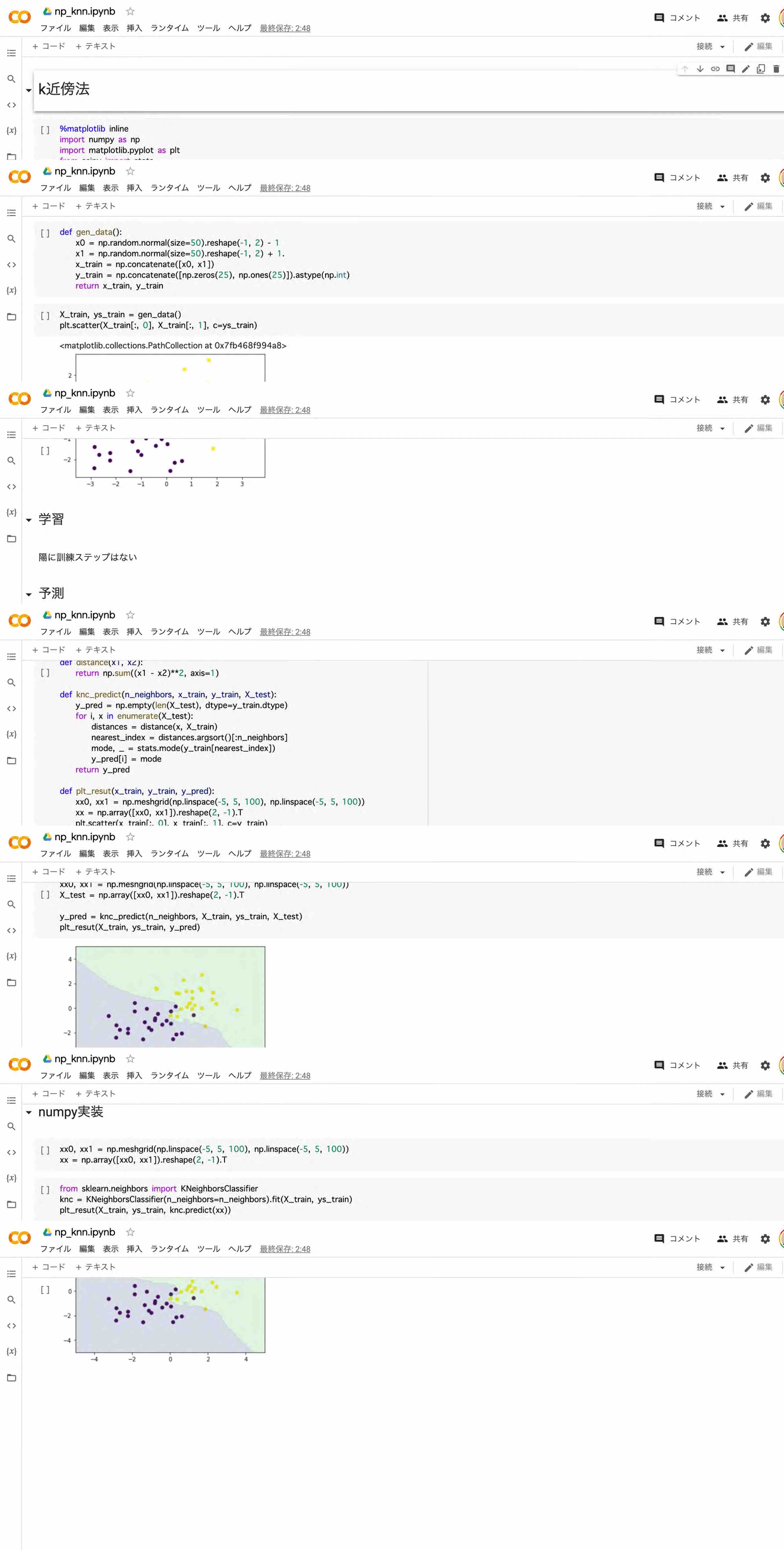
k近傍法

分類に使われる手法の一つで、与えられた学習データをベクトル空間上にプロットしておき、未知のデータが得られたら、そこから距離が近い順に任意のk個を取得し、その多数決でデータが属するクラスを推定するというもの

分類のアルゴリズムの中でも、シンプルでわかりやすいアルゴリズム

ハンズオン

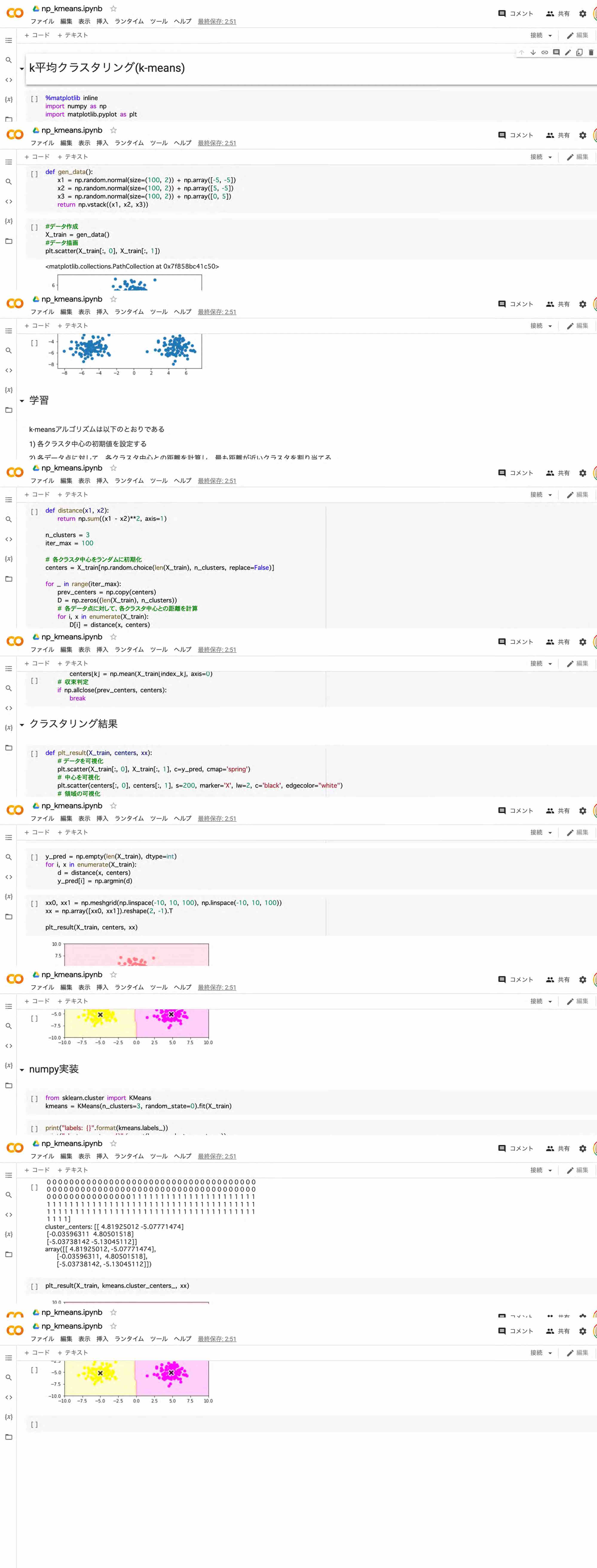
k-means法(k平均法)

非階層型クラスタリングのアルゴリズム。クラスタの平均を用い、与えられたクラスタ数k個に分類する。単純なアルゴリズムであり、広く用いられている。

ハンズオン

6.サポートベクターマシーン

教師あり学習の一種で2分類問題を処理するための手法

境界線に近い点をサポートベクトルと呼び、サポートベクトルを最大化するように、境界線を引くようにする。

2つのクラスに分ける境界線を分類境界という。 それぞれのクラスのデータが分類境界からなるべく離れるようにして「最適な」分類境界を決定する。 分類境界を挟んで2つのクラスがどのくらい離れているかをマージンと呼ぶ。 SVMの視点では、マージンが大きいほど良い分類境界となる。 分類境界に最も近いデータx_iが分類境界を支えていると解釈できるため、このx_iのことをサポートベクトルと呼ぶ。

ハードマージン　：はっきり分類出来る状態 ソフトマージン　：誤判別を許容することを想定

ハンズオン